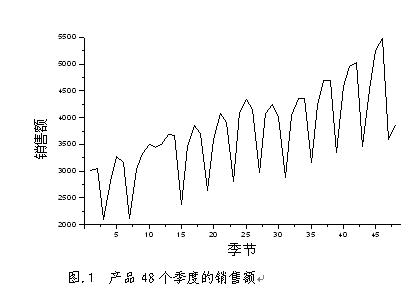
在实际的企业实践中,数据往往是连贯具有时间特征的,因此如果想要做出比较好的预测,特别需要注意时序数据的处理。那么,什么是时序数据,又应该怎么处理,显然需要特别关注。
1. 什么是时序数据
时序数据是指时间序列数据。是按照时间顺序记录的数据列,在同一数据列中的数据必须是同口径的,要求具有可比性。时序数据可以是时期数,也可以是时点数。
比如运满满的经历中,划分数据的时间粒度是天,属于时期数。时点数是指按照记录生成的记录时间,也就是实际时间。
其往往含有下面的特征(这些特征并不需要记住,只需要理解之后,在构造特征的时候可加以考虑):
- 数据是时序的,一定带有时间戳;
- 数据是结构化的,也可能是多模态的;
- 数据可能有更新操作;
- 数据源并不唯一;
- 用户关心的是一段时间后的趋势(或者一段时间后的值);
- 数据存在保留时限(更新时限,即过于早的时间序列数据并不需要);
- 数据可能会较为平稳,也可能存在突变;
- 数据量通常巨大;
基于以上几点原因,我们在处理时序类特征的时候,需要考虑的方面就会比较多。
2. 时序构造特征
2.1 时间序列基本规则法 - 周期因子法
- 如果时间序列周期性比较强,可以尝试计算周期因子,计算base,通过base*周期因子的方式来预测;
- base怎么计算?我觉得可以用平均值、中位数都可以;
2.2 时间特征建模
- 提取时间的周期性特征作为特征,此时无需滑窗截取训练样本。常见方式使用one hot编码:
- 将星期转换为0-1变量,从周一至周天,共七个变量;
- 将节假日转化为0-1变量,可简单分为有或者无,也可以根据具体的节日去构造不同编码值;
- 将月初、月中转换为0-1变量;
- 视具体问题而定,控制时间粒度,改为月、星期、天、小时;
- 更加常见的是,通过时间周期进行滑动窗口动态构造训练集与测试集,例如时间序列的波动呈现明显的周情况,那么可以考虑聚合前一周的特征,然后使用当周期的实际值作为预测值;
2.3 传统时序建模方法,ARMA/ARIMA等线性差分模型
- 不属于我们这里讨论的范畴;
2.4 时间序列分解
- 拆分为长期趋势变动T、季节变动S(显式周期,固定幅度、长度的周期波动)、循环变动C(隐式周期,周期长不具有严格规则的波动)和不规则变动I,参考链接:
- 循环变动C在短期内不体现,可直接归入趋势变化中;
- 季节性分析;
2.5 特征工程+机器学习模型
- 学会构造特征工程,例如一些跟目标值相关的滑窗特征;
- 学会从不同的角度去训练模型,再进行融合堆叠;
- Kaggle某次比赛第一名思路:
2.6 深度学习网络
结合CNN+RNN+Attention,作用不同互相配合
- CNN捕捉短期局部依赖关系;
- RNN捕捉长期宏观依赖关系;
- Attention为重要时间段或者变量加权;
- AR捕捉数据尺度变化;
具体方法:LSTNet、TPA-LSTM
2.7 图像识别方法
将时间序列转换为图像数据,再利用图像模型做分析
- GAF(Gramian Angular Field),将笛卡尔坐标系下的以为时间序列,转化为极坐标表示,再使用三角函数生成GFA矩阵
- 优点:通过半径r表示序列的时间依赖性,极坐标保留时间关系的绝对值,每个序列产生唯一的极坐标映射图;可通过GAF矩阵的主对角线,恢复笛卡尔坐标系下的原始时间序列;
- 缺点:当序列长度为n时,产生的GAF矩阵为n*n,建议分段聚合近似,保留序列趋势,同时减少序列大小;
- Short Time Fourier Transform(短时傅里叶变换STFT)
- 通用的语音信号处理工具;
3. 分割训练测试集
从上面一些方法可以看出,时间序列数据集有时候很难做交叉验证,因为模型通常需要学习时间的长期趋势信息,除非将时序信息处理成特征,加入长期趋势特征,否则几乎不能打乱训练和预测数据的相对时序顺序。
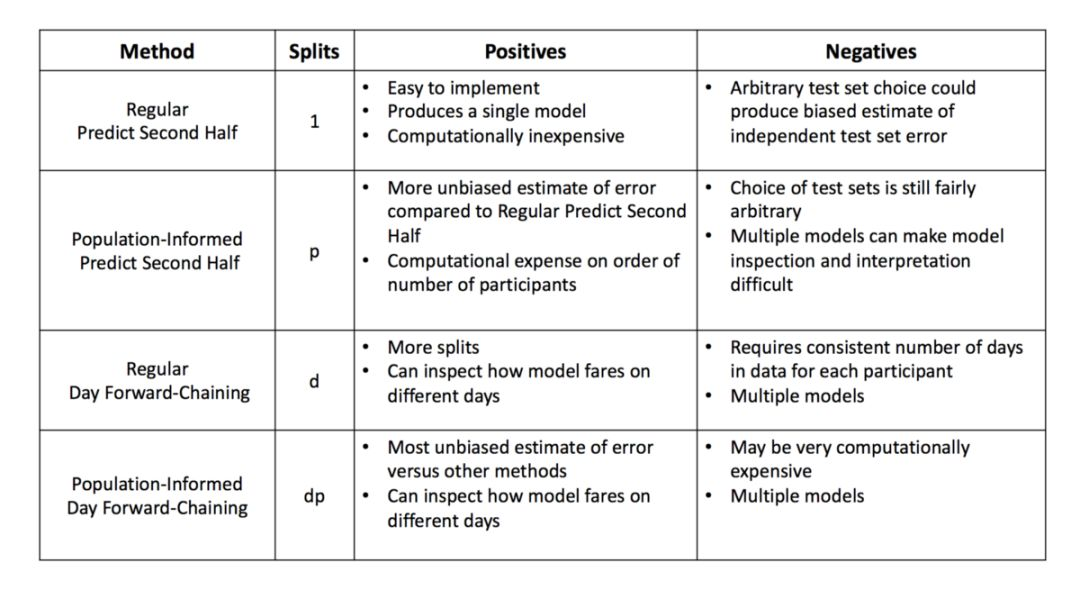
- 按照时间点切割:即随机挑选一个时间点,根据正负样本或者训练、测试样本的数量比,来划分训练测试集;
- 链式时间点切割:即按照训练集(训练子集、验证集)、测试集的方式来生成训练样本,并且按照训练的时间粒度来一个一个递推向前构造训练集;
参考链接:
我个人认为要么采用链式,要么采用滑动窗口的方式,也就是训练集和测试集的大小不改变,随着时间序列向前滑动。
4. 常用的评价指标
- 点预测:对于点指标,常见的MSELoss、MAE、GMAE、RMSE等都可以用,也可以用绝对百分比误差;因为MSE、MAE比较常见,就不做具体的介绍,GMAE指的是误差的累积再开方,RMSE是对MSE进行开方;
- 一般来说,RMSE>MAE>GMAE,也比较清楚地比较了几者的敏感程度;
- RMSE和MAE对异常值比较敏感;
- 概率分布预测:实际使用模型预测类似库存水位的时候,分位数受异常值的影响程度比较低,那么分位数损失可以当成训练目标及评估指标;
- 具体的介绍可以看下面的文章:
- 时间序列预测指标: